The Project Critical Path is the longest path of activities that must be completed in order for the project to be completed. All activities that are on the critical path, if late, will cause delays in the project.
Project managers need to know the critical path as it allows them to:
- Determine the length of the project duration in a more reasonable way.
- Identifying dependency relationships between activities, constraints, and risks on the project.
- Establish a realistic project schedule based on work priorities.
Project managers utilize the critical path method (CPM) algorithm to define the shortest amount of time required to finish each task with the least amount of float.
Project scheduling software equipped with Gantt charts can now automatically calculate critical paths, making the CPM method much easier.
Now that we know about the critical path, we can learn more about the critical path method (CPM), which is based on this concept.
What is CPM and Why Do We Use the Critical Path Method (CPM)?
Project managers use the critical path method (CPM) to create a project schedule and estimate the overall project duration.
The critical path method is a project schedule and estimation technique that’s used to create an accurate timeline of the total duration of a project.
This technique uses a network diagram, which visually represents task sequences or tasks needed to complete the project. Once these are identified, the time frames are calculated to identify the longest path over all paths and its overall time frame.
Critical Path according to PMBOK® Guide 5th Edition:
The sequence of activities that represents the longest path through a project, which determines the shortest possible duration.
History of CPM
Morgan R. Walker and James E. Kelley created the critical path method in the late 1950s.
The two different project management techniques are CPM and PERT.
PERT is suitable for projects where it is not known how long the required activities will take to complete, whereas CPM is appropriate for recurring projects which have a set timeline.
What are the Benefits of Using CPM in Project Execution?
Tasks in a project must follow a set schedule to stay on track by a set deadline. If you don’t do this, the scope of your project will easily run out of control.
The critical path technique is particularly significant in project management since it defines all the tasks required to finish a project. It determines what work must be completed on time which can be delayed if necessary, and how much float or slack there will be.
When done right, critical path analysis can help you in the following ways:
- Estimate the duration of each task more accurately.
- Determine task dependencies, resource constraints, and project risks.
- Prioritize task based on their time float or slack, which helps with project planning and resource allocation.
- Identify important work that cannot be delayed and ensure that it is carried out on schedule.
- Monitor the progress of your project and track any deviations from the timeline.
- Compressing the schedule (on certain activities) after estimating the project completion time in the beginning.
Important Factors of CPM
We must understand the concept of CPM and the variables that affect it before learning how to calculate the critical path with this method.
Relationships between activities: Finish to Start, Finish to Finish, Start to Start, Start to Finish.
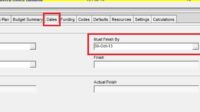
Early Start (ES): this is the earliest start time for an activity in your project. You can’t know until you identify the task dependencies between activities in the project.
Late Start (LS): is the latest time an activity can be started before affecting the project delay.
Early Finish (EF): The earliest finish of an activity that will not affect the overall project schedule.
Late Finish (LF): The latest finish of an activity that will not affect the overall project schedule.
Float: Float, often known as slack, is the word that defines how long a task can be delayed before it impacts the task sequence and project schedule. Since tasks on the critical path cannot be deferred, they have no float (float value 0).
Let’s look at some critical path examples to understand these parts of critical path analysis better.
Critical Path Example
Example by HBR
The following is an illustration of a CPM diagram. It might help you visualize the importance of critical paths to the project timeline, even at a high level.
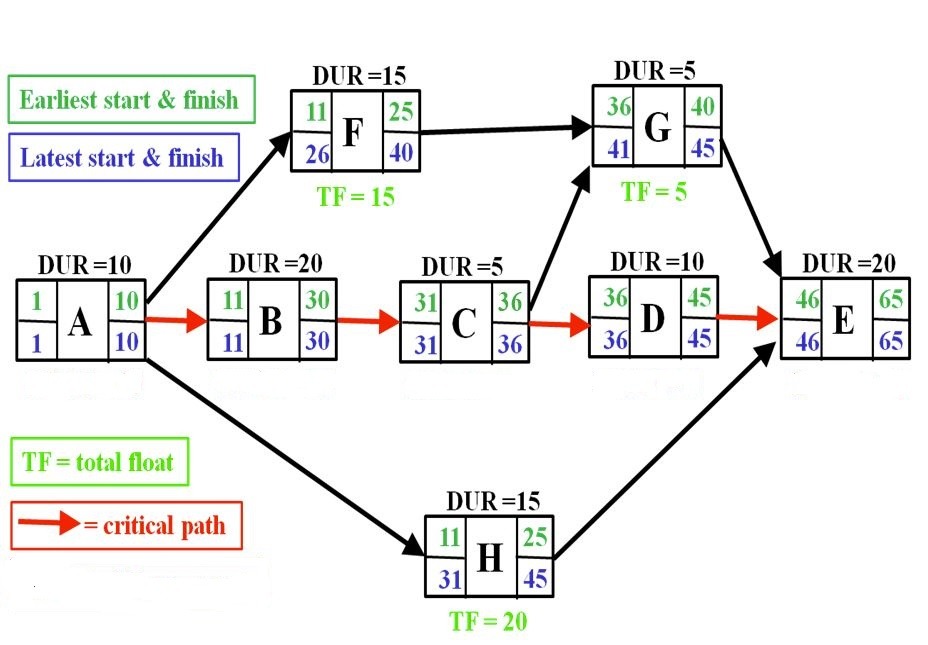
For now, we will use this critical path diagram to demonstrate the components of the CPM approach.
Harvard Business Review provides an example of a critical path schedule.
Now look again at the schedule in the following table:
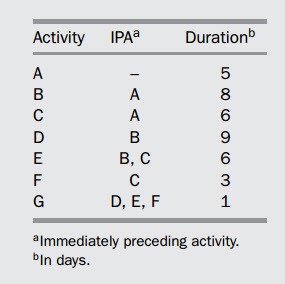
The relationships that can be formed from the activities in the table can be seen in the image below using the Precedence Diagram Method (forward pass and backward pass):
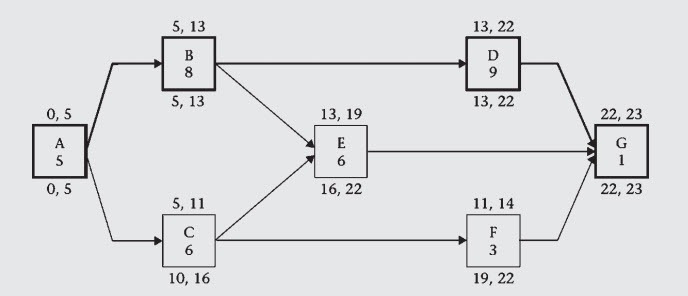
From the image above, it can be seen that the critical path is marked with a bold black color.
Also, read what is the Gantt chart.
Multiple Critical Paths
It may not be common to have more than one critical path, but it is possible for this to happen.
There are a few reasons why there could be more than one:
- Different paths have the same duration.
- Milestones in a constrained project reflect phased handovers/completions/contractual requirements which cause different paths to be critical at the same time.
- Individual schedules, each with their own critical path, combined into an overall master program.
As long as you understand why there are multiple paths and what they’re all about then that’s ok!
Project Management & CPM Software
Project scheduling software did not exist when the critical path method (CPM) was invented, so project managers had to calculate the critical path manually.
Fortunately, several project management software options are available today that can help with critical path processes.
Primavera P6 is one of the most frequently used project management software for identifying critical paths.
Here are some of the key features you’ll need as a project manager to effectively use the critical path method for scheduling:
- Add Activity (start date and duration).
- Creating relationships between activities.
- Create Calendar.
- Displaying float.
- Add Constraints.
- Display critical path with different color.
- Adding resources.
- Saving baseline.
- Actual updates.
- Comparing actual and baseline.
- Doing filtering.
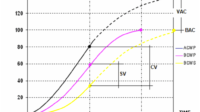
- Showing S-Curve.
- Tracking Historical for schedule change (in Primavera).
- Input Budget.
- Reporting.
Conclution of Critical Path
From the examples above, a conclusion can be made about the Critical Path, which is the longest path of the schedule which consists of a series of activities from the beginning to the end of the project.
Here are some observations about critical paths:
- In every schedule, there must be at least one critical path.
- The critical path can be more than one but it is not recommended.
- Each critical path must be continuous from start to finish of the project.
- Exception: when a constraint is set, the path may be critical from the start to the constraint activity or from the constraint activity until the end.
- Some people define the critical path as a path with a total float of zero. This is true as long as there are activities with a total float of zero from start to finish.
- Some of them define the critical path as the longest path on the schedule (from start to finish). The definition of the critical path is the longest path is more precise in most cases because if the project finish date is made longer, the path with a total float zero will change to positive (more than 0). So the critical path will be the longest path with the least number of total floats.
My work experience includes roles as Project Control, Planner, Scheduler, and more. My responsibilities include fulfilling project manager needs in multinational companies by analyzing and presenting project feasibility related to planning (master schedule), monitoring and coordinating project schedules/progress, conducting delay analysis (EoT - Extension of Time), and mitigation analysis.
- Earned Value Method: What is it and how to use it - December 24, 2023
- What is the Critical Path Method in Project Management - November 23, 2023
- What is Free Float, Total Float, and Lag in CPM - November 19, 2023
